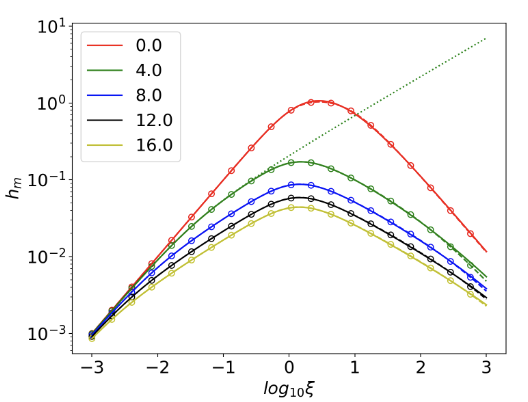
The second-harmonic generation process of a focused laser beam inside a nonlinear crystal is described by the Boyd-Kleinman theory. Calculating the actual conversion efficiency and upconverted power requires the solution of a double integral that is analytically intractable. We provide an expression that predicts the exact gain coefficient within an error margin of less than 2% over several orders of magnitude of the confocal parameter and as a function of the walk-off parameter. Our result allows for readily tuning the beam parameters to optimize the performance of the upconversion process and improve optical system designs.